Clifford algebra
Is the same as Geometric Algebra, but from a different approach.
Let $V$ be a finite-dimensional real (complex) vector space with nondegenerate bilinear form $g$. The (complex) Clifford algebra $Cl(V,g)$ is the algebra generated by $V$ along with the anti-commutation relation
$$ vu+uv =2g(u,v), $$or equivalently with the relation $u^2=g(u,u)$.
Note: the Clifford algebra can be seen like coming from the tensor algebra $T(V)$. The Clifford algebra $\text{C}\ell(V,g)$ is the quotient $\text{C}\ell (V,g)=T(V)/I(V)$ of $T(V)$ by the ideal $I(V)$, generated by the elements of the form $v \otimes u + u \otimes v -2g(u,v)$. This ideal is also generated by $u\otimes u-g(u,u)$. If you take (u+v)⊗(u+v) = u⊗u + u⊗v + v⊗u + v⊗v we have: g(u+v,u+v) = g(u,u)+ u⊗v + v⊗u + g(v,v), and since g(u+v,u+v) = g(u,u) + g(u,v) + g(v,u) + g(v,v), this gives us: u⊗v + v⊗u = g(u,v) + g(v,u) = 2 g(u,v).
If the signature of $g$ is $(p,q)$, then we use the notation
$$ Cl_{p,q} $$or
$$ Cl(p,q). $$Note: If $x,y\in V$, then $xy$ belong to the subset of $Cl(V,g)$ denoted by $V^2$.
Example. $\text{Cl}_{0,2}(\mathbb{R})$ is a four-dimensional algebra spanned by $\{1, e_1, e_2, e_1e_2\}$ which behave like quaternions (note that this is not the only way to see quaternions in the framework of Clifford algebras).$\blacksquare$
Example: Pauli vectors constitute a representation of the Clifford algebra $Cl_{3,0}=Cl(3,0)$, since they satisfy
$$ \sigma_i \sigma_j+\sigma_j \sigma_i=2I\delta_{ij}. $$It is called the Algebra of Physical Space (APS). Its matrix representation is given by the Pauli matrices. It is related to Pauli spinors
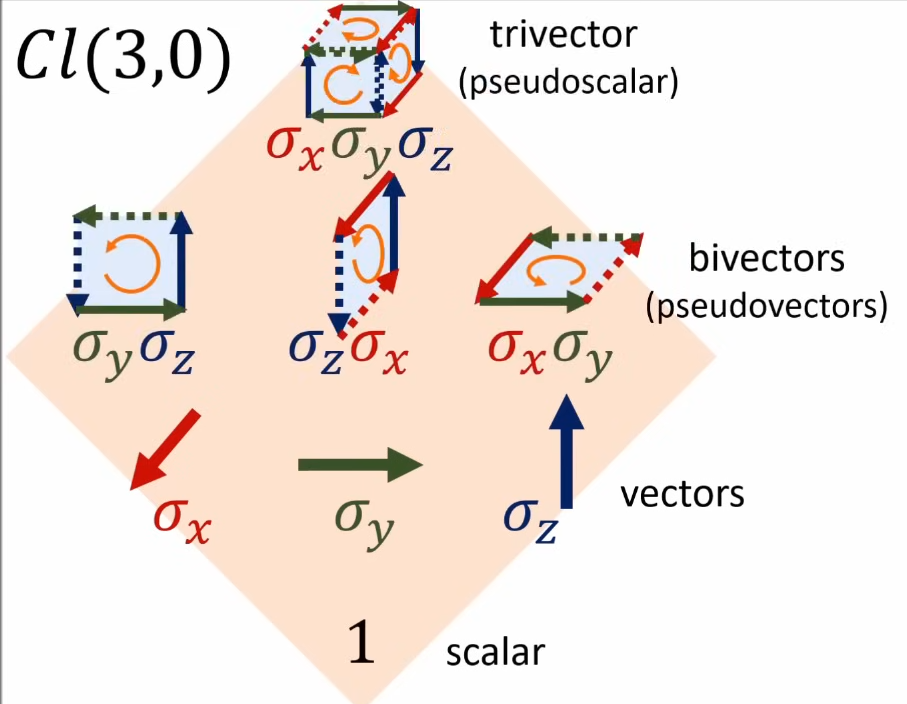
$\blacksquare$
Example: The Clifford algebra $Cl(1,3)$ is called the Spacetime Algebra (STA) and it is related to the Weyl spinors.
$\blacksquare$
Rotations
(see this video
3D Space $Cl(3,0)$, APS
- Rotations in $ij$-plane:
4D Spacetime $Cl(1,3)$, STA
- Rotations in $ij$-plane:
- Boost in $k$-direction:
The spin group and the spinors
Inside the Clifford algebra $Cl(n)$ we can find the spin group $Spin(n)$. In the case $n=3$ (spatial rotations), $Spin(3)$ consists of [Lounesto pag 59]
$$ \operatorname{Spin}(3)=\left\{s \in \mathcal{C} \ell_3 \mid \tilde{s} s=1, \bar{s} s=1\right\} $$where the tilde and the bar denotes reversion and Clifford conjugation [Lounesto page 56].
But additionally, if we consider a minimal left ideal of $Cl(n)$, denoted by $S$, then it is a vector space and we have a natural homomorphism
$$ \rho: Spin(n) \to GL(S) $$given by $\rho(g)(s)=$ [TO BE COMPLETED with Lounesto page 60, for n=3] for $g\in Spin(n)$ and $s\in S$. We have, then, a group representation of $Spin(n)$ called the fundamental representation via Clifford algebra, and the elements of $S$ are called spinors.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: